偏差广泛存在于推荐系统中,使得推荐系统的性能受到了很大的影响,但是各类 bias 的定义和 debias 方法尚未统一。因此本文主要简单介绍下何向南团队关于推荐系统中的 bias 和 debias 的最新综述论文 Bias and Debias in Recommender System: A Survey and Future Directions,这篇论文应该只是放了初稿,还是存在一些的编写错误的,如果阅读原文注意甄别,另外文中的一些介绍是比较晦涩的,需要结合原文阅读。由于我所在的业界是不太关注所谓的公平性这一问题的,所以在我的这篇介绍中基本隐去了原文中关于 fairness 的部分,如果对这方面有兴趣的可以阅读原文。
摘要
近年来,关于推荐系统(RS)的研究论文迅速增长,但大多数论文都集中在设计机器学习模型以更好地匹配用户行为数据这个方向上。然而,用户行为数据是观察性的,而不是实验性的(observational rather than experimental),这使得数据中广泛存在各种偏差(bias),包括但不限于选择偏差、位置偏差、曝光偏差和热度偏差。盲目的拟合数据,而不考虑其内在的偏差,会导致很多严重的问题,如线下评价与线上指标不一致,影响用户对推荐服务的满意度和信任度等。为了将大量的研究模型投入实践中,我们非常迫切的需要探索偏差的影响并在必要时进行去偏(debias)。当我们审阅那些考虑了 RS 中的偏差的论文时,我们惊奇地发现,这些研究往往是支离破碎并且普遍缺乏一个系统的组织。“偏差”这个术语在文献中被广泛使用,但它的定义通常是模糊的,甚至在不同的论文中不一致。这促使我们对现有的关于 RS 偏差的工作做一个进行系统的 survey。在本文中,我们首先总结了推荐中的七种偏差,以及它们的定义和特征。然后我们提供一个分类目录来定位和划分现有的关于推荐系统去偏的工作。最后,我们确定了一些开放的挑战,并展望了未来的方向,希望能激发更多的研究工作在这一重要但容易被忽视的课题。
引言
推荐系统(RS)能够为每个用户提供个性化的建议,被认为是缓解信息过载的最有效的方法。它不仅方便了用户寻找信息,也有利于内容提供商的盈利潜力。如今,推荐技术在无数的应用中得到了广泛的应用,如电子商务平台(阿里巴巴、亚马逊)、社交网络(Facebook、微博)、视频分享平台(YouTube、TikTok)、生活方式应用(Yelp、美团)等等。因此,在这个信息超载问题变得越来越严重的时代,RS 显得至关重要。
RS中偏差具有普遍性
导致偏差存在的几个重要因素有:
- 为推荐模型奠定基调的用户行为训练数据是观察性的,而不是实验性的。主要原因是用户是在曝光的项目(items)上产生行为,使得用于训练的观测数据被系统的曝光机制和用户的真正自我选择所混淆;
- 项目在数据中呈现的并不均匀,例如一些项目比其他项目热度更高,从而获得更多的用户行为。因此,这些高热度的项目将对模型培训产生更大的影响,从而使最终的推荐结果也更偏向于它们,同样的情况也适用于用户侧。
- RS 的一个本质是自璇式反馈循环——RS 的曝光机制决定用户行为,这些行为反过来作为 RS 的训练数据。这样的反馈循环不仅会产生偏差,而且会随着时间的推移而加剧,导致“富人更富”的马太效应。
推荐系统的自璇式反馈循环
如下图一所以,推荐系统可以抽象为三个关键组件:用户、数据和模型的反馈循环,其包含三个阶段:
- 用户 $\rightarrow$ 数据,此阶段推荐系统收集用户集 $U = {u_1, …, u_n}$ 和项目集 $I = {i_1, …, i_m}$ 的 user-item 交互数据以及一些 side information。收集的数据一般有两种形式:1)隐式反馈(implicit feedback),通常用矩阵 $\boldsymbol{X} \in \mathbb{R}^{n \times m}$ 表示,其中的每个元素 $x_{ui}$ 都是二值化的,代表用户 $u$ 是否和项目 $i$ 产生了交互行为(如购买、点击或者浏览);2)显式反馈(explicit feedback),通常用矩阵 $\boldsymbol{R} \in \mathbb{R}^{n \times m}$ 表示,其中的每个元素 $r_{ui}$ 表示用户关于项目的偏好用实值表示(如评分)
- 数据 $\rightarrow$ 模型,根据收集的数据训练模型,其核心是从历史交互行为中获得用户偏好,并预测用户接受目标项目的可能性,这一环节一直是推荐系统中的热点
- 模型 $\rightarrow$ 用户,返回给用户推荐的结果,目标是满足用户的信息需求,此阶段可以影响用户的未来行为及决策。
在这种循环的模式中,用户和 RS 处于相互动态演化的过程中。通过推荐,用户的个人兴趣和行为发生改变;同时,利用更新的用户行为数据,RS 会进入一种自我强化的模式。
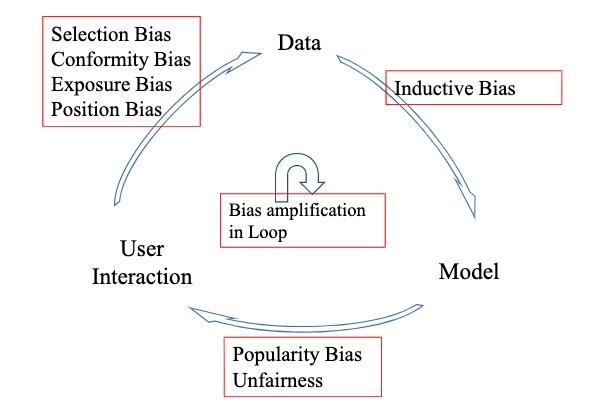
Fig 1. 推荐系统的自璇式反馈循环,导致了偏差的放大,形成马太效应 (Image source: Jiawei Chen et al.)
推荐系统中的偏差
数据中的偏差
由于用户交互的数据是观察性的,而不是实验性的,因此很容易在数据中引入偏差。它们通常源自不同的数据子组,并使推荐模型捕捉这些偏差,甚至扩大它们,从而导致系统性的偏见和次优决策。在此,我们将数据偏差分为四组:选择偏差(selection bias)、从众偏差(conformity bias)、不明确反馈(inexplicit feedback)、曝光偏差(exposure bias)和隐式反馈中的位置偏差(position bias in implicit feedback)。
显式反馈中的偏差(Bias in explicit feedback data)
- 选择偏差(selection bias):源自用户对项目的评分(即明确的反馈),当用户可以自由选择要评分的项目时,就会出现选择偏差,因此推荐系统观察到的评分样本并不能作为所有评分的代表性样本。图 2 展示了 Marlin et al. 的调查统计结果,证明了推荐系统得到的观察性样本是包含固有选择偏差的,这是由于用户的主观性造成的评价数据的非随机丢失(missing not at random)。
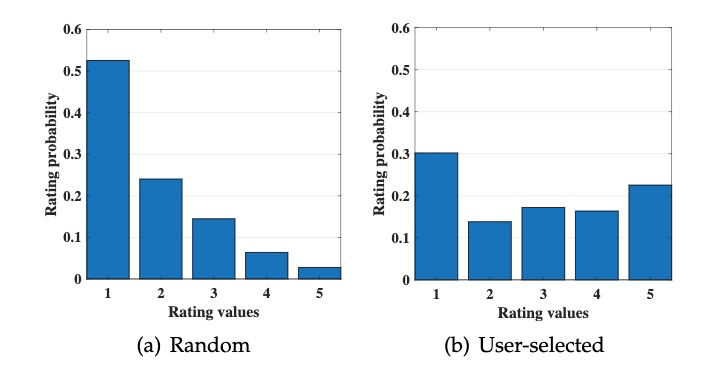
Fig 2. 关于选择偏差的统计结果表明,1)用户更倾向于评价自己感兴趣的项目;2)用户更倾向于评价很好或很差的项目 (Image Source:Marlin et al.)
- 从众偏差(confirmity bias):用户在一个群体中进行评价时倾向于做出和其他人相似的评价,即使这样做违背了他们自己的判断,者使得这些评价并不总是表明用户真正的偏好。例如,受公众的高评价的影响,一个用户很可能会改变他的低评价,避免过于苛刻的,这种从众现象很常见,并且会导致用户评分的偏差,无法反映用户对产品的真实偏好。
隐式反馈中的偏差(Bias in implicit feedback data)
-
曝光偏差(exposure bias):在推荐系统中,由于用户只能接触特定一部分的项目,因此未被观察到的项目并不总是代表用户对它们具有负面偏好。具体来说,用户与项目之间无交互可能有两个原因:1)项目与用户兴趣不匹配;2)用户并不知道该项目的存在(例如手机用户未下滑浏览到该项目)。因此在这种情况下下,很难区分真正的负面交互(曝光给了用户但用户不感兴趣)和可能的正面交互(如未曝光给用户),进而将导致严重的偏差。
根据以往的研究,曝光偏差存在几种不同的形式:1)由于曝光受之前推荐系统策略的影响,因此,一些研究也将这种曝光偏差称为前模偏差(previous mode bias) ;2)由于用户会主动搜索感兴趣的项目,因此推荐系统更可能曝光和用户选择高度相关的项目,在这种情况下曝光偏差又称为选择偏差;3)用户的背景可能影响曝光,例如他的社交朋友圈以及地理位置;4)热门的项目也更容易曝光给用户,因此热度偏差也是一种曝光偏差的形式。为了统一用词,以上的偏差类型在下文统称为曝光偏差。
-
位置偏差(position bias):位置偏差的发生是由于用户倾向于与推荐列表中位置靠前的项目进行交互,而不考虑这些项目的实际相关性,因此发生交互的项目可能并不是高度和兴趣相关的。Maeve et al. 指出用户通常会信任推荐列表中的前几个结果,然后停止评估其余的项目。因此,从用户对推荐列表的反馈中收集的数据可能不能完全反映用户的喜好。因此,在训练和评估阶段位置偏差都带来了挑战。
模型中的偏差
偏差的存在并不是完全有害的,为了达到一些特性, 我们会在模型中特意加入一些归纳偏差(inductive bias)。归纳偏差是指模型为了更好地学习目标函数并泛化到训练数据之外而做出的假设。泛化能力是机器学习的核心之一,如果没有事先对数据或模型的假设,就无法实现泛化,因为测试集样本可能有一个任意的输出空间。类似地,构建推荐系统需要对目标函数的性质进行一些假设,例如,我们假设可以通过嵌入表示的内积来预估交互概率。除了目标函数之外,在其他方面也可以添加归纳偏差,例如 “自适应负采样器” 它的目的是对 “困难” 样本(hard sample)进行过采样,以提高学习速度。另一个例子是离散排序模型,它将用户和项目作为二进制编码嵌入,以提高推荐的效率,但也牺牲了表达能力。
偏差与结果的公平性
除了数据和模型中的偏差,还有两种常见的偏差。
-
热度偏差(popularity bias):受欢迎的商品被推荐的频率甚至比它们受欢迎的程度还要高。
长尾现象在 RS 数据中很常见:在大多数情况下,一小部分受欢迎的热门项目占据了大部分的用户互动。当对这种长尾数据进行训练时,模型通常会给特定热门项目比理想值更高的分数,而简单地将不热门的项目预测为负数。因此,受欢迎的热门项目被推荐的频率甚至比它们在数据集中表现出的受欢迎程度还要高。如下图 3,显示了项目热度和推荐频率之间的关系,我们可以发现,大多数推荐的产品都位于高人气区(H),但事实上,它们被推荐的程度甚至远远超过了它们最初的人气。
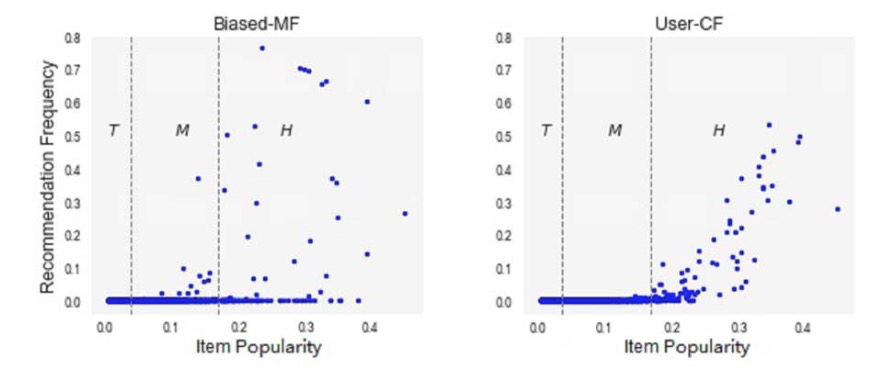
Fig. 3 在 Biased-MF 和 User-CF 中项目热度和被推荐频率的关系图,项目被分为三组,H 表示高热项目占据了大约 20% 的评论,T 表示不热门的项目也有约 20% 的评论,M 表示剩余的项目 (Image Source:Abdollahpouri et al.)
热门偏差会损害用户的个性化体验,降低推荐结果的公平性(fairness),同时还会进一步增加热门项目的曝光度,恶性循环形成马太效应。
-
不公平性(Unfairness):RS 系统性、不公平地歧视某些个人或群体而偏袒其他人。特别是,基于种族、性别、年龄、教育水平或财富等属性,不同的用户群体通常在数据中表现不一。当基于这种不平衡的数据进行训练时,模型很有可能获得这些 over-represented 群体,在排名结果中强化它们,并可能导致系统性歧视,降低弱势群体的可见性(例如,对 under-represented 的少数群体具有种族或性别相关的刻板印象)。
反馈循环与偏差
真实世界的推荐系统通常会产生一个不利于推荐系统的反馈循环,前面的小节总结了在循环的不同阶段出现的偏差,而这些偏差会随着循环的推移而进一步增强。以位置偏差为例,热门项目通常会从更大的流量中获益,这反过来会提高它们的排名突出度和它们收到的流量,从而导致马太效应。许多研究者也研究反馈循环对热度偏差的影响并发现反馈循环会放大热度偏差,热门物品会变得更受欢迎,而非热门的物品会变得更不受欢迎。这些被放大的偏差也会减少多样性,加剧用户的同质化。
Debiasing 方法
一、针对选择偏差的方法
1. Debiasing in evaluation
一般我们会选用平均绝对误差(MAE)、均方根误差(MSE)、折损累计增益(DCG@k)以及精确度(Precision@k)作为评估的指标,遵循以下范式:
\[H(\hat{R})=\frac{1}{n m} \sum_{u=1}^{n} \sum_{i=1}^{m} \delta_{u, i}(r, \hat{r})\tag{1}\]其中,\(\delta_{u, i}(r, \hat{r})\) 根据不同的指标而取相应的计算方法,如对于 MSE,\(\delta_{u, i}(r, \hat{r}) = (r_{u,i}-\hat{r}_{u,i})^2\),而 \(r_{u,i}\) 和 \(\hat{r}_{u,i}\) 分别表示用户 \(u\) 关于项目 \(i\) 的真实评价值和预估评价值。然而,对于推荐系统来说,式(1)仅在观测到的数据上进行计算,存在用户带来的选择偏差。针对这个问题,目前有两种策略。
-
倾向分(propensity score):为了在 evaluation 阶段弥补选择偏差,一些工作提出可以类比病人与药物的关系,采用一种在观测样本上进行逆倾向分加权(weighting with inverse propensity score)的方法。对于一个 user-item 对 $(u, i)$ 倾向分 $P_{u,i}$ 定义为观测评分的边缘概率 $\left(P_{u, i}=P\left(O_{u, i}=1\right)\right)$,以此来抵消选择偏差,此时在观测数据上新的估计可以视为理想指标的无偏估计: \(\begin{gather} \hat{H}_{I P S}(\hat{R} \mid P)=\frac{1}{n m} \sum_{(u, i): O_{u, i}=1} \frac{\delta_{u, i}(r, \hat{r})}{P_{u, i}}\tag{2} \\ \begin{aligned} \mathbb{E}_{O}\left[\hat{H}_{I P S}(\hat{R} \mid P)\right] &=\frac{1}{n m} \sum_{u} \sum_{i} \mathbb{E}_{O u, i}\left[\frac{\delta_{u, i}(r, \hat{r})}{P_{u, i}} O_{u, i}\right] \\ &=\frac{1}{n m} \sum_{u} \sum_{i} \delta_{u, i}(r, \hat{r})=H(\hat{R}) \end{aligned}\tag{3} \end{gather}\)
-
ATOP: ATOP 是另一种无偏指标,其包含两个温和(mild)假设:1)观测数据中会随机缺失相关的 / 高(relevant / high)评价;2)对于其他评分,我们允许一种任意的数据丢失机制,只要它们丢失的概率比相关的评分高。其定义如下: \(\begin{aligned} \mathrm{TOPK}_{u}^{\mathrm{obs}}(k) &=\frac{N_{u}^{+, \mathrm{obs}, k}}{N_{u}^{+, \mathrm{obs}}} \\ \mathrm{TOPK}^{\mathrm{obs}}(k) &=\sum_{u} w^{u} \mathrm{TOPK}_{u}^{\mathrm{obs}}(k) \\ \mathrm{ATOP}^{\mathrm{obs}} &=\int_{0}^{1} \mathrm{TOPK}^{\mathrm{obs}}(k) d k \end{aligned}\tag{4}\) 其中,$N_{u}^{+, \mathrm{obs}}$表示观测到的用户 $u$ 的相关评分个数,$N_{u}^{+, \mathrm{obs}, k}$ 表示前 $k$ 个推荐结果中相关评分个数,Steck et al 证明 $\text{ATOP}_u^{obs}$ 是 average recall 的无偏估计。
小结:倾向分和 ATOP 是两种精心设计的策略,但仍然存在两个致命缺点:对于前者,仅在真实倾向分可获取的情况下才能保证是无偏估计的;而对于后者,只有当两个假设成立时,才能保证 ATOP 的无偏性。在实践中,随机丢失机制往往是复杂的,导致假设并不总是有效的。
2. Debiasing in model training
-
数据插补(data imputation):选择偏差的出现是由于用户具有任意评价的权力,因此一种直接的策略就是除了预测用户的评分外,还可以考虑一个数据丢失预测任务,例如预测哪些项目用户会选择评价。这种策略背后的假设是,用户选择项目的概率取决于用户对该项目的评分值。然而这种多任务的训练方式可能比较复杂,还可以使用一些数据插补的策略来替代,可以直接对缺数数据插入一个特定的评分值 $r_0$,并用以下目标函数优化模型:
\[\underset{\theta}{\arg \min } \sum_{u, i} W_{u, i} \cdot\left(r_{u, i}^{o \& i}-\hat{r}_{u, i}(\theta)\right)^{2}+\operatorname{Reg}(\theta) \tag{5}\]其中,$r_{u, i}^{o \& i}$ 表示观测数据或插入的评分,\(\hat{r}_{u, i}(\theta)\) 表示在参数 \(\theta\) 下的预测评分,\(W_{u,i}\) 用于对插入数据进行降权。但是,无论是丢失预测模型还是评分插值模型是采用启发式的方法,这类方法会由于预测或插值的不准确而造成经验误差,这种不准确性会传播到推荐模型训练中,降低模型性能。
-
倾向分(propensity score):在模型的训练中还可以直接考虑倾向分并优化如下的经验损失函数:
\[\underset{\theta}{\operatorname{argmin}} \sum_{O_{u, i}=1} \frac{\hat{\delta}_{u, i}(r, \hat{r}(\theta))}{P_{u, i}}+\operatorname{Reg}(\theta)\tag{6}\]其中,$\hat{\delta}_{u, i}(r, \hat{r}(\theta))$ 可以是原始的评估函数或是任意可以优化的替代函数,最后一项是正则化项。然而,正如前面小节所讨论的,指定适当的倾向分是至关重要的,模型性能取决于倾向分的准确性。此外,基于倾向分的方法通常会遭受 high variance 问题,难以取得最佳结果,特别是当数据中项目的热度或用户活跃度高度倾斜时。
-
双重鲁棒模型(doubly robust model):数据插值的方法容易受到插值的精确性影响,倾向分的方法受 high variance 影响,因此有人提出结合两种方法以获取双重鲁棒性,即如果插值或倾向分有任意一项是准确的,就可以让模型保持无偏差的能力,并定义了以下目标函数:
\[\mathcal{E}_{\mathrm{DR}}=\mathcal{E}_{\mathrm{DR}}\left(\widehat{r}, r^{o}\right)=\frac{1}{n m} \sum_{u, i}\left(\hat{e}_{u, i}+\frac{o_{u, i} d_{u, i}}{\hat{p}_{u, i}}\right)\tag{7}\]其中,\(\hat{e}_{u, i} = \delta_{u, i}(r_0, \hat{r}_{u,i})\),表示预测分和插值分的损失,而 \(d_{u,i}=\hat{e}_{u,i}-\delta_{u,i}(r,\hat{r})\) 表示插值损失与真实损失的偏差。虽然该模型比单一方法更鲁棒,但仍需要相对准确的倾向分或插值数据,而这些数据通常难以精准获取的,性能任然会受到影响。
-
元学习(meta learning):为了解决上述方法高度依赖倾向分和插值的问题,Saito et al 提出了一种基于非对称 tri-trianing 框架的元学习方法。他们首先用两个特定的推荐模型预训练两个预测算子(A1, A2),以生成具有伪评分(pseudo-rating)的可靠数据集,最后根据这个数据集训练一个目标推荐模型 A0。其理论分析表明,该方法优化了理想损失函数的上界。然而,非对称 tri-training 的性能取决于预训练的预测器 A2 的好坏。当 A2 表现较差时,上界可能会 loose,导致 A0 的结果也是次优的。事实上,从有偏差的数据中学习一个高质量的 A2 是具有挑战性的。A2 通常存在选择偏差,而选择偏差最终会注入到目标推荐模型 A0 中。然而,元学习和上界优化是减轻选择偏差十分有前途的方向,值得进一步探索。
二、针对从众偏差的方法
从众偏差是指用户通常会受到他人意见的影响,从而使评分值偏离用户的真实偏好。人们提出了两种方法来解决从众倾向。
第一种工作认为用户评分符合民意,Liu et al 直接采用了三个重要特征 $c_{ui},a_{ui},d_{ui}$ 输入到一个基础的推荐模型得到一个基础预测分 $t_{ui}$,并通过一个权重 $\omega$ 控制其可信度,最后再通过 Xgboost 模型得到最终的预测分:
\[\hat{r}_{u i}=x g b\left(\left\{(1-\omega) \cdot t_{u i}+\omega \cdot a_{u i}, c_{u i}, d_{u i}\right\}, \Theta_{x g b}\right) \tag{8}\]另一种工作认为用户评分是用户偏好和社交影响的综合结果,类似第一种方法,他们引入社交因子作为基础推荐模型的输入,并同样用一个权重控制其影响。
三、针对曝光偏差的方法
1. Debiasing in evaluation
一种非常直接的方式就是采用类似消除选择偏差时所使用的倾向分的方法,Yang et al 首先抽象出了在隐式反馈数据上的理想推荐评估:
\[R(\hat{Z})=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\left|\mathcal{S}_{u}\right|} \sum_{i \in \mathcal{S}_{u}} c\left(\hat{Z}_{u, i}\right) \tag{9}\]其中,\(\hat{Z}_{u, i}\) 表示为用户 \(u\) 预测出关于项目 \(i\) 的排名,\(\mathcal{S}\) 表示用户在全局项目集 \(\mathcal{I}\) 中的偏好项目集,函数 $c(\cdot)$ 可以自适应的变为任意评估指标,例如 AUC 指标 \(c\left(\hat{Z}_{u, i}\right)=1-\dfrac{\hat{Z}_{u, i}}{\|\mathcal{I}\|}\),然而曝光偏差的存在导致仅有部分用户偏好的项目被展示,使得模型是在观测结果上进行有偏评估:
\[\begin{aligned} \hat{R}_{\mathrm{AOA}}(\hat{Z}) &=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\left|\mathcal{S}_{u}^{*}\right|} \sum_{i \in S_{u}^{*}} c\left(\hat{Z}_{u, i}\right) \\ &=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\sum_{i \in S_{u}} O_{u, i}} \sum_{i \in S_{u}} c\left(\hat{Z}_{u, i}\right) \cdot O_{u, i} \end{aligned}\tag{10}\]其中, \(S_{u}^{*}\) 表示曝光给用户的偏好项目集,但最终导致 \(\mathbb{E}_{O}\left[\hat{R}_{\mathrm{AOA}}(\hat{Z})\right] \neq R(\hat{Z})\)。为了解决这个问题,Yang et al 同样提出了对观测样本进行逆倾向分加权(weight with inverse propensity score)的 IPS-based 方法,目的是为了对观测到的样本进行降权,并提升罕见样本的权重:
\[\begin{aligned} \hat{R}_{\mathrm{IPS}}(\hat{Z} \mid P) &=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\left|\mathcal{S}_{u}\right|} \sum_{i \in S_{u}^{*}} \frac{c\left(\hat{Z}_{u, i}\right)}{P_{u, i}} \\ &=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\left|\mathcal{S}_{u}\right|} \sum_{i \in S_{u}} \frac{c\left(\hat{Z}_{u, i}\right)}{P_{u, i}} \cdot O_{u, i} \end{aligned}\tag{11}\]这样,就可以得到一个无偏的评估即,\(\mathbb{E}_{O}\left[\hat{R}_{\mathrm{IPS}}(\hat{Z} \mid P)\right] = R(\hat{Z})\)。
2. Debiasing in model training
为了从隐式反馈中提取负向信号解决训练中的曝光偏差,一种传统的策略是把所有未观测到的用户交互作为负样本并为它们指定一个置信度。大多数这类方法的目标函数如下:
\[\min _{\theta} \sum_{u, i} W_{u i} \delta\left(x_{u i}, \hat{r}_{u i}(\theta)\right)+\operatorname{Reg}(\theta)\tag{12}\]其中,\(x_{ui}\) 表示 user-item 对 \((u,i)\) 之间的交互值,\(\delta(\cdot)\) 表示预测结果 \(\hat{r}_{ui}(\theta)\) 和真实反馈结果 \(x_{ui}\) 之间预定义的损失函数如交叉熵损失,\(W_{ui}\) 表示置信权重,置信权重的指定至关重要,大致可以分为三类:
-
启发式:加权矩阵分解(WMF)和动态矩阵分解(dynamic MF)就使用了一种简单的启发式方法,对于未观测到的交互统一分配一个较低的权重;另一种启发式的方法则是设置一个正比于用户的活跃度的权重,其背后的思想是交互更多项目的用户的置信度更高;类似地,项目的热度也可以被考虑入权重分配的过程,因为越热门的项目曝光机会越高;还可以考虑用户和项目的特征相似度作为分配的依据。
Saito et al 提出了一种利用用户偏好的启发式损失函数:
\[\mathcal{L}_{\text {ideal }}(\theta)=\frac{1}{n m} \sum_{u, i}\left[r_{u, i} \delta\left(1, \hat{r}_{u, i}\right)+\left(1-r_{u, i}\right) \delta\left(0, \hat{r}_{u, i}\right)\right]\tag{13}\]每一对 user-item 交互都通过用户的偏好级别 $r_{ui}$ 加权,并进一步提出了一个基于倾向分的替代评估:
\[\begin{aligned} \hat{\mathcal{L}}_{\mathrm{sur}}(\theta) &=\frac{1}{n m} \sum_{u, i} \left[x_{u i}\left(\frac{1}{P_{u i}} \delta\left(1, \hat{r}_{u, i}\right)+\left(1-\frac{1}{P_{u i}} \delta\left(0, \hat{r}_{u, i}\right)\right)\right)+\left(1-x_{u, i}\right) \delta\left(0, \hat{r}_{u, i}\right) \right] \end{aligned}\tag{14}\]当倾向分 $P_{ui}$ 定义为用户曝光于项目的边缘概率时,式(14)可以作为理想损失函数的无偏估计。然而,分配合适的置信度权重在理论上是具有挑战性的,因为对于不同的 user-item 交互来说,最优的数据置信度是变化的。选择置信度权重或倾向分通常需要先验经验或消耗大量计算资源进行网格搜索。此外,手动为数百万数据设置个性化的权重是不现实的,而粗粒度的人工置信权值在估计用户偏好时会产生经验偏差。
-
采样:采样决定哪些样本会参与更新模型参数及参与的频率。给定一个样本的采样概率 $p_{ui}$,训练带抽样的推荐模型等价于训练带有以下加权目标函数的模型:
\[E_{(u, i) \sim p}\left[\delta\left(x_{u i}, \hat{r}_{u i}(\theta)\right)\right]=\sum_{u, i} p_{u i} \delta\left(x_{u i}, \hat{r}_{u i}(\theta)\right)\tag{15}\]其中,采样分布扮演的是数据置信度权重的角色。采样策略在很多模型中都很有效,包括 NCF、LightGCN。我们可以对热门的负向项目进行过采样,因为这些热门项目更可能被曝光。然而,启发式的采样方法不足以捕捉真实的负样本分布,所以我们可以引入 side information 来增强采样器。例如,对被浏览但未被点击的数据来评估用户曝光;结合社交网络的信息进行采样;构建基于项目的知识图谱,并在图上进行采样。
-
Exposure-based model:我们还可以设计一个可以捕捉用户曝光于项目可能性的 exposure-based model。EXMF 引入了一个曝光变量并假设隐式数据的生成过程如下:
\[\begin{aligned} a_{u i} & \sim \text {Bernoulli}\left(\eta_{u i}\right) \\ \left(x_{u i} \mid a_{u i}=1\right) & \sim \text {Bernoulli}(\hat{r}(\theta)) \\ \left(x_{u i} \mid a_{u i}=0\right) & \sim \delta_{0} \end{aligned}\tag{16}\]其中,$a_{ui}$ 表示一个用户是否被曝光于项目,$\delta_0$ 表示 delta 函数 $p(x_{ui}=0\mid a_{ui}=0)=1$,其可以通过一个很小的值参数化为伯努利分布,$\eta_{ui}$ 表示曝光的先验概率。当 $a_{ui}=0$ 时,有 $x_{ui}\approx 0$,因为此时用户无法与项目交互。而当 $a_{ui} = 1$ 时,用户知道了这个项目,用户会基于自己的偏好选择是否交互。通过优化 $x_{ui}$ 的边缘概率,模型可以自适应的学习曝光概率,进一步转化为置信权重来弥补曝光偏差。EXMF 的目标函数可以简写为:
\[\sum_{u i} \gamma_{u i} \delta\left(x_{u i}, \hat{r}_{u i}(\theta)\right)+\sum_{u i} g\left(\gamma_{u i}\right)\tag{17}\]$\gamma_{ui}$ 表示用户曝光的可变参数,$g(\gamma_{ui})$ 是由可变参数决定的函数:
\[g\left(\gamma_{u i}\right)=\left(1-\gamma_{u i}\right) \ell\left(x_{u i}, \varepsilon\right)+\ell\left(\gamma_{u i}, \eta_{u i}\right)-\ell\left(\gamma_{u i}, \gamma_{u i}\right)\tag{18}\]其中,$\ell(a, b)=\operatorname{alog}(b)+(1-a) \log (1-b)$,可以发现,$\gamma_{ui}$ 指示了一个用户有多大可能曝光于项目,并作为置信权重来控制数据在模型训练中的贡献。这一发现与我们的直觉相符,只有当用户已经接触到该项目时,他才能根据自己的偏好决定是否消费该项目。因此,越高曝光率的数据得出的用户偏好越可靠。
进一步说明 exposure-based 模型是如何弥补曝光偏差的,以下图 4 有向图为例,推荐模型的本质是在估算如果项目被曝光给用户后,一个用户是否会购买此项目。也就是说,我们要估算概率 $p\left(x_{u i} \mid d o\left(a_{u i}=1\right), \theta, \eta\right)$,根据因果推断中的后门准则,有 $p\left(x_{u i} \mid d o\left(a_{u i}=1\right), \theta, \eta\right) = p\left(x_{u i} \mid a_{u i}=1, \theta, \eta\right) = p(\hat{r}(\theta))$,所以推荐模型的性能确实反映了推荐的效果。
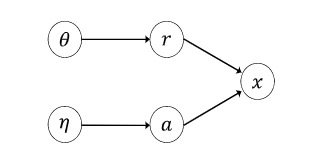
Fig. 4 一个任意的 exposure-based 的 graph. (Image Source:Jiawei Chen et al.)
然而,直接从计算式(17)估计数据的置信度是不够的,由于推断参数 $\gamma$ 的规模太大,模型容易出现过拟合/无效的问题。
四、针对位置偏差的方法
1. 点击模型
一些点击模型有一个假设:如果一个展示的项目被用户点击了,那么它一定是被(用户)检验过且相关(examined and relevant)的。为了弥补位置偏差,这些模型显式的建模用户在位置 $p$ 点击项目 $i$ 的概率:
\[\begin{array}{l} P(C=1 \mid u, i, p) =\underbrace{P(C=1 \mid u, i, E=1)}_{r_{u i}} \cdot \underbrace{P(E=1 \mid p)}_{h_{p}} \end{array}\tag{19}\]这里,应用了一个隐藏随机变量 $E$,表示用户是否检验过该项目,用户是否检验一个项目仅与该项目所在的位置 $p$ 有关。这个公式类似 exposure-based 模型,只不过建模的对象是位置而不是曝光概率。
另一些点击模型属于级联模型(cascade model),与上述的模型的不同之处在于,它将单个 query 会话中的点击和跳过聚合到单个模型中。它假设用户会从第一个项目检验到最后一个项目,点击取决于项目的相关性。我们用 $Ep$,$\ Cp$表示第 $p$ 项是否被检验和点击的概率事件。级联模型通过以下方式生成用户点击数据:
\[\begin{array}{l} P\left(E_{1}\right)=1\\ P\left(E_{p+1}=1 \mid E_{p}=0\right)=0 \\ P\left(E_{p+1}=1 \mid E_{p}=1, C_{p}\right)=1-C_{p} \\ P\left(C_{p}=1 \mid E_{p}=1\right)=r_{u_{p}, i} \end{array} \tag{20}\]式(20)中的第三个式子表明,如果一个用户找到了他感兴趣的项目,那么他会结束会话,反之,他总会继续检验。级联模型假设在每个query 过程只有一次点击,如果一个项目被用户所检验,则该项目被点击的概率为 $r_{u_p,i}$,并以 $1-r_{u_p,i}$ 的概率跳过。通过考虑个性化转移概率或利用深度循环生存(recurrent survival)模型,可以对基本的级联模型进行进一步改进以更深入地考虑用户的浏览行为。
然而,这些点击模型通常需要对每个 query-item 或 user-item 对大量的点击数据,这使得它们在点击数据高度稀疏的系统中难以应用。此外,一旦错误地描述用户点击的生成过程,将会引入经验偏差并损害推荐性能。
2. 倾向分(Propensity Score)
倾向分仍然可以应用到位置偏差中,通用的损失函数形式定义如下:
\[\begin{array}{l} L_{I P W}(S, q)=\sum_{x \in \pi_{q}} \Delta_{I P W}\left(x, y \mid \pi_{q}\right) \\ =\sum_{x \in \pi_{q}, o_{q}^{x}=1, y=1} \dfrac{\Delta\left(x, y \mid \pi_{q}\right)}{P\left(o_{q}^{x}=1 \mid \pi_{q}\right)} \end{array}\tag{21}\]其中,$S$ 表示排序系统,$q$ 表示所有 queries 集 $Q$ 中的一个 query 实例,而 $\pi_q$ 表示根据 $q$ 从 $S$ 中检索出的排序结果,$x$ 是排序结果中的一个 document,$y$ 是 0-1 变量表示 $x$ 和 $q$ 是否相关,$\Delta\left(x, y \mid \pi_{q}\right)$ 用于计算每个相关项目上损失的函数,$P\left(o_{q}^{x}=1 \mid \pi_{q}\right)$ 表示在排序结果中观察到结果 $x$ 和 $q$ 相关的边缘概率也即倾向分。
由于仅仅依赖于项目的位置,基于倾向分的方法发展较好,一种非常简单有效的方法就是对结果进行随机化,先对排序结果随机化再收集用户的点击数据以计算倾向分。因为在所有位置上的项目相关性是相同的,可以证明,不同位置上的点击率的差异产生了真实倾向的无偏估计。尽管结果随机化很简单且有效,但却有可能严重损害用户体验,因为排名较高的项目可能不受用户欢迎。因此,Fang et al 和 Agarwal et al 探索了在不干预推荐结果的情况下,从数据中学习倾向分的策略,但需要从多个排序模型中获取反馈数据。
五、针对热度偏差的方法
1. 正则化
合适的正则化方法可以让推荐结果更均衡,LapDQ 正则化项 \(tr(Q^T L_D Q)\) 中,\(Q\) 表示项目的嵌入矩阵,\(L_D\) 是 \(D\) 的 Laplacian 矩阵,\(D_{ij} = 1\) 如果项目 \(i\) 和 \(j\) 属于相同的集合(例如热门或长尾项目) ,\(tr(\cdot)\) 表示矩阵的迹。Kamishima et al 提出了基于 mean-match 正则化项,他们首先引入互信息来度量特征对推荐结果的影响,并推导得到一个特别的正则化项:\(-\left(\boldsymbol{M}_{D^{(0)}}(\{\hat{r}\})-\boldsymbol{M}_{D^{(1)}}(\{\hat{r}\})\right)^{2}\),其中 \(\boldsymbol{M}_{D}(\{\hat{r}\})=\frac{1}{\|D\|} \sum_{\left(x_{i}, y_{i}, v_{i}\right) \in D} \hat{r}\left(x_{i}, y_{i}, v_{i}\right)\) ,\(D\) 表示训练集,\(x,y\) 分别表示用户和项目,而 \(v\) 是引入的一个 viewpoint 值用于增强推荐结果的中立性,\(v\) 的取值可以受多个方面影响,例如和用户相关的性别、年龄等以及和项目相关的发布日期等,也可以是和用户和项目交互的时间戳等。
上述正则化方法都是面向结果的,Chen et al 提出了一种面向过程的方法,其假设长尾分布的项目由于很少和用户发生交互,所以他们的嵌入向量训练的不够充分,因此他们提出了一种迁移学习的方法 ESAM,试图将 well-trained 项目的知识迁移到长尾项目上。
2. 对抗学习
对抗学习在解决热门偏差时的基本思想是,在推荐器 G 和对抗器 D 之间进行 min-max game,这样 D 可以改善对小众(niche)项目推荐的性能,在Krishnan et al 提出的方法中,D 的输入包括合成 popular-niche 项目对 $\tilde{i}^{p}, \tilde{i}^{n} \mid u)$ 以及相同数据量的真实 popular-niche 项目对 $\left(i^{p}, i^{n}\right)$,后者是从全局共现统计矩阵中采样得到的,而合成对是从推荐器 G 中生成得到的。推荐器 G 可以用任意推荐模型(如 NCF)实例化。通过 G 和 D 之间的对抗学习,D 可以学习热门项目和小众项目之间的隐含关联,而 G 可以学习如何捕捉更多与用户历史相关的小众项目,从而为用户推荐更多的小众项目。
3. 因果图(causal graph)
Zheng et al 通过因果推断来解决热门偏差,他们假设用户的点击行为取决于兴趣和项目的受欢迎程度,并构建了一个特定的因果图,如图 5 所示,为了区分用户兴趣和热门偏差,考虑了两种嵌入方式:兴趣嵌入捕捉用户对项目的真实兴趣,热度嵌入捕捉由热度引起的伪兴趣。在多任务学习框架下,这些嵌入可以用特定的 cause-specific 数据进行训练。最后,热度偏差被解除的兴趣嵌入向量将被用于最终推荐。
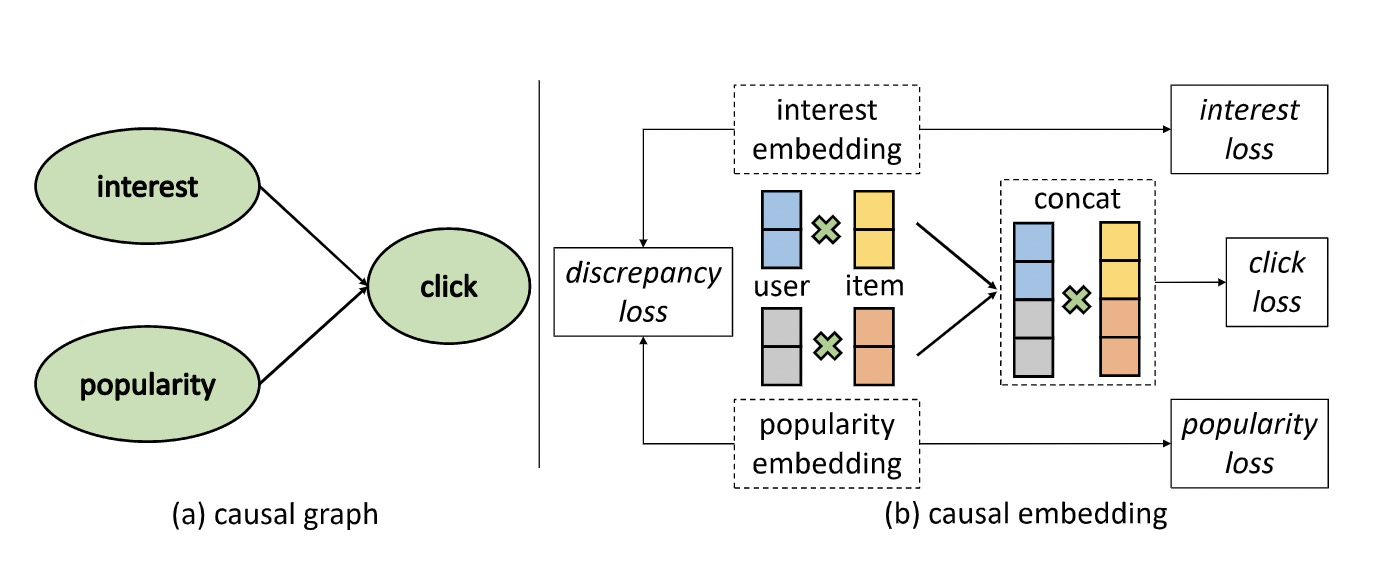
Fig. 5 因果图与因果嵌入 (Image Source:Zheng et al.)
六、针对反馈循环带来的偏差放大
1. 均匀数据(Uniform Data)
收集均匀数据是解决偏差循环放大问题的最直接的方式,对于每个用户,并不直接根据推荐模型给出结果,而是随机选择一批项目并按照均匀分布去排序。均匀数据通常提供了无偏差信息,因为它打破了反馈循环,不受各种偏差的影响。然而,均匀策略不可避免地会损害用户的体验和平台的收益,因此它通常被限制在一小部分在线流量。因此,如何用较小的均匀数据校正偏差是一个关键的研究问题。
2. 强化学习
随机收集均匀数据并不是一个令人满意的策略,因为它会损害推荐性能。因此需要探索更明智的推荐策略,推荐系统中存在探索-挖掘(exploration-exploitation)的困境,探索是随机推荐商品并收集无偏差的用户行为数据以更好地捕捉用户偏好,而挖掘是推荐预测出最符合用户偏好的商品。为了解决这个问题,大量的工作通过构建强化学习 (Reinforcement Learning) agent 来开发交互式推荐。图 6 展示了在 RL agent 下的系统-用户交互。与传统的推荐方法不同,RL 将信息搜索任务视为 RL agent(系统)和用户(环境)之间的顺序交互。在交互过程中,agent 可以根据用户的历史信息或反馈(state $s_t$)不断更新策略 $\pi$,并生成与用户偏好最匹配的项目列表(action $a_t$),或探索用户偏好以获得长期回报。然后,用户会对推荐给出反馈(reward $r_t$,如评价或点击),因此,RL 能够平衡探索与挖掘之间的关系,最大化每个用户对系统的长期满意度。
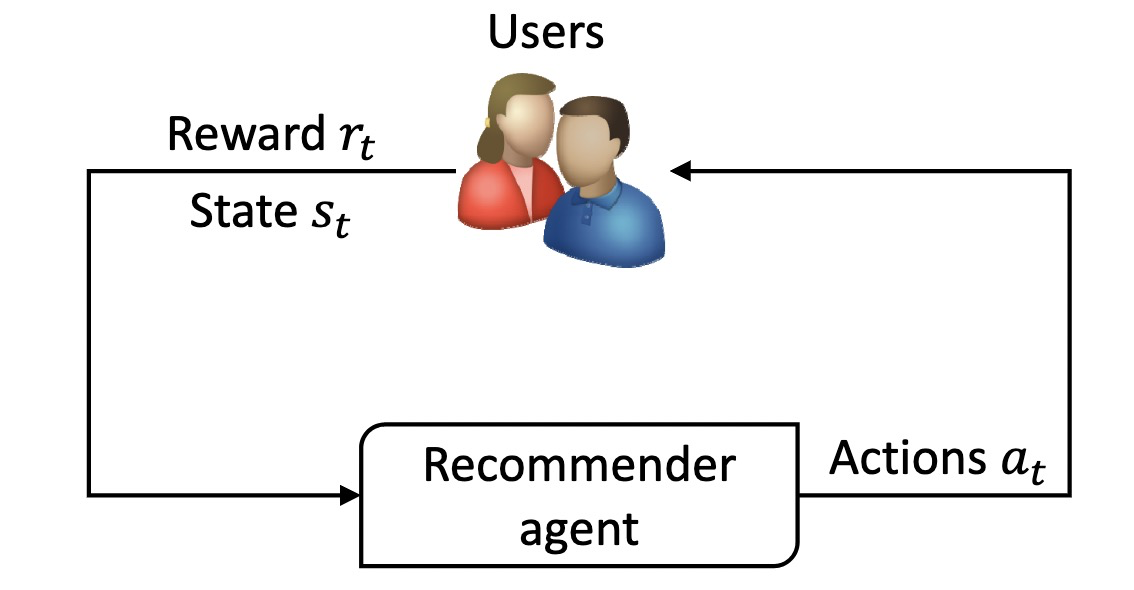
Fig. 6 系统-用户在强化学习 agent 下进行交互 (Image Source:Zhao et al.)
基于 RL 的推荐的一个挑战是如何评估一个策略的好坏。最好方法是直接以 AB test 的形式在线上部署,然而,从工程和逻辑方面来说,既昂贵耗时且当策略如果不成熟时,可能损害用户体验。政策外评估是一种替代策略,它使用历史交互数据来评估新政策的表现。然而,非策略评估会受到偏差的影响,因为使用现有的有偏差的日志记录策略而不是统一策略来收集数据。
未来工作
倾向分的评估
如前所述,逆倾向得分是一种常用的去偏差策略。然而,只有当正确指定倾向得分时,这种策略的有效性和无偏性才能得到保证。如何获得正确的倾向得分一直是一个重要的研究问题。现有的方法通常假定理想倾向分是给定的。尽管在一些简单的情况下(如位置偏差)对倾向分数的评估已经进行了探索,但在更复杂的情况下(如选择偏差或曝光偏差)对倾向分数的评估仍然是一个有待解决的问题。
通用的 Debias 框架
从以前的研究中,我们可以发现现有的方法通常只是设计用于解决一两个特定的偏差。然而,在现实世界中,各种偏差往往同时发生。例如,用户通常会对自己喜欢的物品进行评分,而他们的评分值会受到公众意见的影响,在收集的数据中,从众偏差和选择偏差混杂在一起。此外,被打分的 user-item 对的分布往往倾向于热门物品或特定的用户群体,这使得推荐结果容易受到热门偏差和不公平性的影响。推荐系统需要一个通用的去偏框架来处理混合的偏见,这是一个很有前途的领域,但在很大程度上还有待探索。
倾向分及它的变体已经成功地应用于各种偏差,是解决这个问题的非常有前途的解决方案。总结不同倾向分在不同偏差上的应用,并提供了一个通用的倾向分学习算法,探索一个新的基于倾向分的框架将是有趣和有价值的。
Debias 方法的评估策略
如何以一种无偏差的方式评估推荐系统?这是该领域的研究者和实践者都必须考虑的问题。现有的方法要么需要精确的倾向分,要么依赖于相当数量的无偏数据。然而,前者的准确性无法保证,而后者损害了用户体验,通常受到很小比例的在线流量的限制。均匀数据提供了最标准的无偏差信息,但由于其规模小,方差大,不足以对推荐模型进行全面评估。利用大规模偏差数据和小规模无偏数据探索新的评估者将是一个有趣的方向。预计还会有更多的理论研究来分析新的评估策略的期望、界限和置信度(expectation、bounds and confidence)。由于受热门偏差和不公平的影响,评估会出现很多困难。不同的方法通常采用不同的评估标准来衡量热门偏差或不公平性,这造成了结果的不一致性。因此,我们认为应该提出一套基准数据集和标准评估指标体系。
Knowledge-enhanced debias
利用丰富的辅助信息来提高去偏的效果是很自然的一个 debias 方向。近年来,就有关于利用用户或项目的属性来纠正推荐中的偏差的方法。一个有趣的方向是如何更好地利用这些辅助信息,因为属性之间不是孤立的,而是相互联系的,这自然可以形成一个知识图谱。知识图谱捕获了更丰富的信息,有助于理解数据偏差。例如,假设用户 $u_1$ 观看电影 $i_1$ 和 $i_2$,这两部电影都是由同一个人 $p_1$ 导演的,属于同一类型 $p_2$。从知识图谱中,我们可以推断,$u_1$ 极有可能知道与实体 $i_1、i_2、p_1$ 或 $p_2$ 有关的电影,这种关联信息对于暴光偏差矫正是很重要的。知识图谱的另一个优点是它的通用性,所有类型的数据、数据源和数据库都可以用知识图表示和操作。
因果图的解释推理
因果图是一种有效的数学工具,用于从数据中阐明潜在的因果关系,从知识和数据的组合中导出因果关系,预测行为的影响,并评估对观察到的事件和场景的解释。因此,对于推荐中的去偏任务,该算法具有很高的应用前景。一方面,debias 的关键是对推荐模型或数据的偏差的发生、原因和结果进行推理。在因果图中,大多数偏差可以用原因假设和额外的混杂因素来理解。偏差的影响也可以通过因果图中的偶然路径推断出来。另一方面,推荐通常被认为是一种干预,类似于用特定药物治疗病人,需要进行反事实推理。如果向用户公开推荐的项目,会发生什么情况?因果图提供了回答这个问题的可能性。公式化的无偏推荐标准可由因果图导出。
如今,做出可解释的推荐变得越来越重要,因为它有助于提高 RS 的透明度、说服力、有效性、可信度和满意度。可解释推荐和去偏差在某种意义上是高度相关的,它们都解决了为什么的问题:它们都需要回答为什么特定的项目会被算法推荐。当因果图有望解决偏差问题时,也可以从图中的强因果路径给出可解释性。我们相信因果模型将把推荐研究带入一个新的前沿。
Dynamic Debias
在现实世界中,偏差通常是动态的而不是静态的。例如,服装的时尚性变化频繁,用户每天都会体验到很多新物品,可能会结交到新朋友;推荐系统将定期更新其推荐策略等等。总之,偏差往往会随着时间的推移而演变。探讨偏差如何发展,分析动态偏差如何影响 RS,将是有趣和有价值的。